Battleground Schools

I have had the opportunity to chat with a teacher sponsor for the volleyball team I coach at Richmond High Secondary.  She just started teaching grade 8 math this year and she said its absurd as to how uniformed her students are in math.  This idea of math phobia is problematic especially to elementary school teachers as they are more generalized.  The teacher sponsor said that often times elementary school teachers will just simply ignore and spend very few hours on mathematics because they themselves have "math phobia".  In her case there is a huge discrepancy between the background knowledge of students when the enter highschool.  It's hard to catch the "lacking" students up with the students who had a solid elementary teacher.  I am sure I will come across similar situations in my teaching career and I am unsure of where and how to begin attacking a problem like this?

After reading battleground schools article it is pretty clear that there has been an ongoing debate between progressive and conservative views of mathematics.  These concepts relate heavily to the relational and instrumental concepts we have inquired about previously in class.  Starting from the progressivist reform era we had an instrumental prevalence.  Dewey then came along and introduce a relational view and since then it has been a back and forth war between the two.  The main part that concerns me is the binary view.  There is no middle ground or grey areas.  Its all black and white(progressive and conservative).  Personally, I think the solution is a combination of both.  As a student, you need the practice, repetitions, strict methods etc.  But you also need the inquiry, abstract, and problem solving skills.  They compliment each other. 

This worries me from a teaching perspective. Does our curriculum allow incorporation of both progressive and conservative?  Do our textbooks do so?  Will I always have to go along with the norm at the present time be it progressive/conservative or am I constrained to just the one path? Also these cycles from left to right don't benefit teachers in anyway.  It becomes a problem if a teacher grows up being taught instrumentally but is then asked to teach relationally or vice versa.

I hope there will be enough time and breathing room to engage students from both sides of the coin but I feel as if I will be forced one way or the other.           

Weight Scale Problem

A market vendor sells herbs in whole number amounts from 1 to 40 grams.
Using an old fashioned 2 panbalance and just 4 weights, she can measure any amount needed.
what are the 4 weights?

This problem turned out to be quite the challenge for me.  Although not directly stated in the question it should be noted that weights can be put on either side at any given time.  So for example if you had a 10kg weight and a 15 kg weight you could put the 10 on one side and the 15 on the other, then add 5g of herbs to balance it.  So we know that we need to find 4 weights in which their additive, subtractive, and counter parts contain all integers from 1-40.

I assumed we needed a 1g weight.  I then made a chart with all the numbers on it from 1 - 40 just so I could keep in check which numbers I needed to get.

From there I did a very methodical but time consuming procedure to find out the answer.

Since we already have a 1g weight, we can cross off 1 from our list.  Now we need to satisfy 2.  We can do this by either adding another 1g weight(1+1 = 2), 2g weight, or 3g weight(3-1 =2).  I decided to go with 3 because it was the furthest away from 1.

So now we can cross off 1,2(3-1),3, and 4(3+1) from our list.

Next we want to cross off 5 from our list.  We can do this by adding a 2g weight(2+3=5), a 4g weight (4+1=5), a 5g weight, a 6g weight(6-1=5), a 8g weight(8-3=5), or a 9g weight (9-(3+1)=5).  I decided to go with 9 because it was the furthest away from 3.

So now we can cross off all the way from 1-13 because we have 1,3,9g weights.

5(9-1-3)
6(9-3)
7(9+1-3)
8(9-1)
9
10(9+1)
11(9+3-1)
12(9+3)
13(9+3+1)

Now we need to cross off 14-40.
We know that we need 4 weights that will add up to 40.  So if we already have 1,3,9 what do we need to get 40?  1+3+9+x=40
                          x=27

Now we can cross off all the numbers from 1-40 because we have 1,3,9,27g weights.

This was the only way I could think of approaching this problem and it happened to work out after a decent amount of time spent plugging and chugging.

After seeing the answer 1,3,9,27 it's clear that these are 3^0, 3^1, 3^2, 3^3.  I tried to find a relation/reason for that but I couldn't figure it out.

Teacherly notes

It might not seem obvious at first but being able to recognize that both sides of the pan can be used is clearly essential to this problem so I think this should be stated in the problem.  This problem was really difficult for myself so I don't know if I can really give too much teacherly advice.

An extension could be
A market vendor sells herbs in whole number amounts from 1 to x grams.
Using an old fashioned 2 panbalance
what are the minimum amount of weights needed to find to measure any amount needed?

Relational Understanding and Instrumental Understanding

After reading Skemps article I can see that both relational mathematics and instrumental mathematics have their pro's and con's.  In a perfect world I think most teachers would agree that relational mathematics is more beneficial to students in the long run.  It allows for better adaptation skills to new problems, offers alternate way's to solve problems, and is cemented in our memory for longer.  Those are just a few to name.   However, the problem is that the world is not perfect.  I don't think relational mathematics is practical from a teaching perspective.  There isn't enough time to describe the why's of every formula, our curriculum is to heavy to do so, and it's substantially harder to test for.  Also if we start to give up some in class time to teach relationally, then we must me giving up some time to teach other subject areas.  From a practical point of view, I think instrumental teaching is far more realistic.  In addition, Skemps states that instrumental mathematics is a quicker and easier way of boosting self confidence in students than relational!  I think self confidence plays a huge role in learning for any discipline, not just math.  This definitely appeals to me as a teacher candidate.  I hope to be wrong though, maybe we do have the time and resources to integrate relational understanding and I am just unaware of it?  And I am sure there are other methods of boosting self confidence in students than instrumental understanding.

Another point brought up in Skemps article was the fact that most teachers use instrumental mathematics and in obvious relation, most students have an instrumental understanding.  So how can we expect our teachers to be more relational if they themselves haven't been taught in a relational way?  Also should we even be thinking in such a binary way(Relational vs instrumental).  Maybe it's optimal to have a blend of both.  I am sure many teachers already teach in a blended fashion.  There are topics that are easily explained relationally and for those that are substantially harder they most likely resort to instrumental to meet curriculum standards in a timely manner.  So while I think that relational understanding is the most desired, instrumental understanding seems more practical and is suffice enough for most students.  Personally I hope to blend both into my teaching.

One final thought I had was that regardless of the way they students were taught, a lot of them may resort to a instrumental understanding anyways just because it is so much easier and quicker to learn that way.  So even if we try to teach relationally, students might learn instrumentally anyways.

True instrumental understanding :)

Memory & Autobiography

Throughout my years as a student I had 2 teachers who were the most memorable.

The first one was my grade 9 math teacher.  Every single class he would bring his guitar and play a tune for us for the first 3 or 4 minutes of class.  To this day I still don't know the "educational" purpose of it.  Maybe it was to calm us down, get our attention, maybe it was even some form of pavlovian conditioning, or maybe it was just the fact that he enjoyed playing the guitar.  Either way it was memorable.  One other thing that he did, whether on purpose or not, was he constantly made errors and mistakes.  He would write up a problem on the board, start doing it, and then halfway through he would realize that he was doing it wrong and he would start over.  It provided some much needed laughter and comfort in knowing that not everyone is perfect.

The second one was my grade 12 math teacher.  The way she taught was very structured, organized, simple, and for the most part pretty standard.  Nothing to fancy, nothing to dull.  But the main thing I remember is that she presented the concepts in such a clear way that I rarely found myself looking in the textbook or going on the internet for a better understanding.  Maybe the concepts were just easier in grade 12?  Or maybe I just started trying harder? But I find it weird that I struggled so much in grade 8 but had no problems in grade 12.  If there is anything I have gained from her, it's that sometimes less is more.  I think as teachers we often get caught up and want to do too much.  From a students point of view this can be overwhelming and stressful so we need to take a step back and keep it simply.  Although my grade 12 teacher may have been pretty "standard," the clarity she provided was unlike any other.   

1000 Lockers and 1000 Students!

A school has 1000 lockers and 1000 students on the first morning of term, all the lockers are open.
Everystudent walks in one by one.
The first student walks in and closes every locker
student number 2 opens every second locker
the third student changes the state of every third locker(opens the closed ones and closes the open ones)
4th student changes every 4th locker... and so on

Once all 1000 students have completed this process, which lockers are closed and why?

First of all lets take a look at what it takes for a locker to be closed or open.  

For a locker to be open we need it to be changed an even number of times because all the lockers started open.  For a locker to be closed we need it to be changed an odd number of times.

So if we changed a locker an even amount of times, lets say 4 times, then it would 

open(because every locker starts open)

closed(1st time changed)

open(2nd time changed)

closed(3rd time changed)

open(4th time changed)

If we changed a locker say 3 times it should be clear that it would end up closed.

So now we need to figure out which lockers will be changed an even amount of times vs the lockers that will be changed a odd amount of times.

Lets take a look at a couple of examples to try and tackle this

Take locker 10 for example.

We know that locker 10 started open (because every locker started open), then it was closed because student #1 closed it, then it was open because student #2, then closed because of student #5, and then finally opened because of student #10.  Each locker is changed by the number of factors(he numbers it is divisible by) it has.  So 10 has factors (1,2,5,10).  Because this is an even amount of factors, in our case there is 4, we know that the locker will end up open.

Now take locker 16 for example.  We know its factors are (1,2,4,8,16).  This is an odd number so we know the locker will end up closed.

How do we know which numbers have an even amount of factors? And which ones have an odd amount?

To answer that we need to look at how factors work.  

Every number has factors that are paired up.  So for example 10 has (10x1,1x10,2x5,5x2).  These pairings produce an even number of factors.  Can you think of a case in which this isn't always true?  If you are having trouble, take a look at the number 16 for example.  16 is a perfect square so we have all the pairs plus the square itself. So 16 has (1x16,16x1,8x2,2x8) and (4x4).  In all the other cases the factors are paired up, producing an even number.  With perfect squares we get an odd number because the factors are paired up except for the square itself.  Still don't get it?  The image below may help you understand it a bit better!

So in conclusion all the numbers that are perfect squares will be closed so 1,4,9,16,25......961.  

and every non perfect square will be open.

Some teacherly notes:

If students are having trouble I think it would be a good idea to pair them up or set them into groups.  This task seems better suited for teamwork!

To challenge your students you can ask them other relevant questions such as
How many times does locker x get changed / touched?
Which locker gets changed the most?
Which locker/s are touched exactly 4 times? etc.

TPI response

To start things off, the results of my TPI test were as follows.

Nurturing was scored the highest(Dominant Perspective)
Apprenticeship and transmission were second highest.
Developmental and Social Reform were the lowest. (Recessive perspective)

I think Mathematics is a very intimidating subject. One of my goals as a teacher is to rid students of this intimidation factor and to inform them that making mistakes and going through failure happens to everyone  so providing a nurturing environment is key.  Lots of students lose self-confidence and self-esteem because of failure and making mistakes, but all of the most well known mathematicians have gone through several failures before achieving success.  Often times without failure there would be no success.  I think that is why I scored so high on the nurturing perspective.

I was surprised my developmental score was so low simply because I hope to be a teacher that gets to know my students on a personal level.  I want to be able to adapt to my students ways of thinking and their level of knowledge.  This is very important to me.  So I am not sure why I scored low?  Maybe I am just not as familiar as to how I should achieve this in a classroom setting?
I think I scored lowest on social reform because I put more emphasis on providing qualitative content in an effective and clear way rather then putting am emphasis on social values and ideologies.  I think Other disciplines such as social studies or English have an easier time of putting more value into social reform.  But again, I hope to learns ways in which I can use this in my lessons as I am unclear as how to do so currently.  The best thing about being a teacher, or becoming a teacher is that we are always evolving as we learn more.

 

Response to Thurston's Article

After Reading Thurston's article I think the main thing I appreciated was his emphasis on communication. Not only in the way we present mathematical concepts but also in a social setting. As Thurston says “Human thinking and understanding do not work on a single track” Different methods of communication benefit different types of people in different ways. I will definitely try to utilize different methods of communicating into my classroom by adding visuals, using metaphors, analogies, and incorporating “motion.” Another point made by Thurston that stood out to me is that its important we don’t assume prior knowledge as this may cause unwanted barriers. Not everyone has the same “mathematical mental infrastructure.” We as teachers need to identify and react to this accordingly by putting a greater emphasis on educating the basics of math and using effective means of communication. Also we need to enjoy the social settings of mathematics! I think too often we get into a narrow minded way of thinking and we treat math as a solo project. We should be expressing our ideas to other people and digesting theirs. Using a social environment to our advantage.

One of the big points that caught my attention was how Thurston implied that most people didn't really care much about the actual proof itself, or rather the results. However it was the understanding that played a greater importance. I’m on the fence to agree if that is still true in an elementary or secondary setting? In my experience, a lot of students just simply want to know the answer :)

Nonetheless I have a different outlook on why we teach and how we should teach mathematics. Putting more of an importance on things that I otherwise would have neglected.

Newspapers and Math??

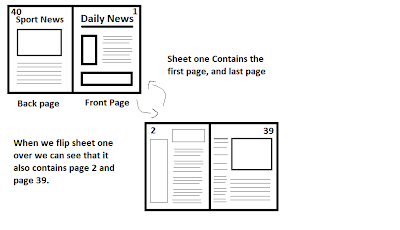
In reading a newspaper, you notice that 4 pages of a section are missing.  One missing page is pg.13.  The back of this section is pg.40

What are the other 3 missing pages?

My first step was to figure out what a newspaper is and how the pages are organized.  A newspaper is constructed by stacking sheets of paper on top of each other and then folding it in half.  Therefore each sheet  of paper contains 4 pages.  Having a hard time visualizing this? Simply grab a few pieces of paper, stack them on top of each other and then fold it in half.
So in our example this first sheet would contain pages 1,2,39, and 40.

Now that we know how a newspaper actually works lets tackle the problem at hand.

Since 40 pages is a relatively low number we can just work our way through all the sheets until we get to page 13

We already know the first sheet contains pages (1,2,39,40).  So the second sheet will contain (3,4,37,38)
and so on
(5,6,35,36)
(7,8,33,34)
(9,10,31,32)
(11,12,29,30)
(13,14,27,28)

So our answer would be pages 14,27,28!
Easy enough.
But what if we said there was 1000 pages and one missing page was page 217?  So the first sheet would contain pages (1,2,999,1000) and we need to find out (217, ?, ?, ?)

I'm way to lazy to write out each section one by one!

Here's a faster way.  We should be able to see that page 218 will also be included because the starting page of each sheet contains the next page as well. Also based on our previous example, page 5 goes in hand with page 6, page 7 with 8, all the way to page 217 with 218.  So now we have (217,218, ?, ?).  We can figure out the rest easily if we just subract 217 from the last page.  1000-217 = 783.  And then we can figure out the last page because 783 goes in hand with 784.

so we get (217,218,783,784)

We can do this subtraction because we already know how a newspaper is organized.  However many pages we go in from the front must mean we go the same amount of pages from the back.

A few words of teacherly advice:

If a student is having trouble
            - I think most students would have trouble visualizing how the newspaper is organized.  So if that is the case then simply just bring in a physical newspaper and show them!
           

Some ways to extend this problem
            - Increase the page numbers
            - Try removing a page that is past the "halfway" mark


           
       

           

Thoughts on proofs

Is Mathematical proof important in mathematics? Why/why not?

Is Mathematical proof important in secondary school math teaching & learning? Why/why not?

I think proofs play a very important role in mathematics.  Its how we can show our peers, colleagues and ourselves that a concept or theory is in fact true.  Proofs are the basic building blocks of math.  We need to be able to understand and use proofs so that we can build and expand on them.  Everything in math builds and relies on eachother, there is a lot of crossover between different fields of math. Proofs make us able to do just that.

Is it important in secondary education? I'm not so convinced that it is absolutely necessary but it's definitely something that we should try to incorporate into our lessons.  Secondary students are always curious as to why we do certain things in math?, why certain concepts are true?  And its important, if we can, to explain to them why.  Sometimes though proofs can be too complex for even a teacher to fully understand let alone a student.  While it is vital to mathematics, it is not vital to secondary education.  If and when we can use proofs in an understanding matter to students we should do so.  But being able to learn the fundamentals and concepts in secondary math doesn't rely on proofs.

First Assignment!

How many sqaures in a 8x8 chessboard?


My thought process behind this was to first identify which types of sqaures could possibly be in the chessboard.  Everything from a 1x1, 2x3, 3x3...... to an 8x8 sqaure. The next step was to figure out how many of each type there are. Once we do that we can simply add them up to get our answer!

For starters I looked at the 1x1 type squares.  It's pretty clear that there is a total of 64.  The reasoning is because there are 8 possible positions vertically and 8 possible positions horizontally.  8x8 = 64.


I applied this same method to all of the different types.  So for a 2x2 type we can see that there is 7 possible positions vertically and 7 possible positions horizontally.  We are limited to 7 because we would go "outside" the board otherwise.  so 7x7 = 49

After applying this method to all types, I ended up with

64 1x1's
49 2x2's
36 3x3's
25 4x4's
16 5x5's
9  6x6's
4  7x7's
1  8x8's

Add them all up and you get 204!

A few words of teacherly advice:
 For students who are stuck or having a difficult time:
               - Add a visual representation or visual aid, this helps a lot!
               - Show them that there is more then just 1x1 squares, 64 is not the answer!

Ways to expand this problem:
               - What happens if the 8x8 chessboard gets bigger or smaller? (ex. 7x7 or 9x9)
               - Other shapes(rectangles, triangles)

Hope you all enjoyed

Thanks :)

First blog

Hey everyone this is my first blog post