Unit Plan

Polyhedra Project

Strengths:  The Polyhedra project is a unique way to incorporate geometry, history, and art all into a mathematics classroom.  I think this could be a great introduction/hook project to start off a geometry unit because it has a non numerical and non formulaic approach.  Also, there is endless creativity options for the construction the origami models(Colours, materials, pictures etc).  For the typical math phobes, this could be an effective way to ease their way into geometry.  The artistic and historic type students will find themselves within their comfort zone and for that reason, they may find this project quite appealing and want to do further inquiry on Polyhedrons.  After finding the mathematical relations they might even be more motivated in the mathematics classroom.  For those who are comfortable with your standard homework, crunching out numbers,formula's, and problem sets, this type of project will certainly push them outside of their comfort zone which offers a beneficial challenge to them.  I think in particular, the writing portion of the project is extremely beneficial because we often neglect to do any writing in mathematics and it is such an important life skill.  Also, the presentation part of the project is great because it allows for all of the students in the class to have some knowledge on all of the topic areas.  You end up creating experts in specific fields, but at the end of the project most of the students will have the general knowledge of all the topics.

Weaknesses:  I thought some of the weaknesses of the project was that while there was certainly an artistic and written portion, there seemed to be very little in terms of the actual mathematics.  To a certain extent the historical component achieves this, for example, Euler's polyhedral theorem, but I don't think it offers enough in terms of PLO's and IRP's.  

Modifications, adaptations, extensions:  I think if I were to use this project in my class I would try and modify it to include less of a historical component while having a bigger emphasis on certain mathematical concepts, like surface area for example.  Personally, I think history is important because it offers interesting stories and it may provide a greater appreciation for mathematics, but at the same time, it can become quite boring and hard to find reliable information.  We also found that building five models is actually quite time consuming, especially if you are adding a lot of creativity, so depending on the group sizes you may want to cut down the number of models students have to build.   

For our project we decided to incorporate both surface area and an very basic introduction into probability by turning the polyhedra models into dice.  We also decided to cut out the historical component because we felt that geometry is already an interesting topic without it.  Possibly some of the "drier" topics will better be suited for history.  In addition, instead of having the students do all five of the origami models, we only required two for each pair.  We thought this might be better because on the presentation day, not everyone will have seen all the different types, providing some variety in the classroom.     

New math project outline  EDCP342A Names: Roz and Travis Project title: Polyhedra Dice
Grade level	Grade 9
Purpose	determine the surface area of composite 3-D objects to solve problems To investigate, create, and present findings on regular polyhedra. Introduction and inquiry into basic probability
Description of activities	Students will first be divided into pairs The pairs will then receive two of the four regular polyhedra (Not including tetrahedron) and be required to re-create a 3-D paper model.  Instructions will be provided on how to create the models. Each pair will then number each face/side of the polyhedra to create a set of dice. The pairs will then come up with a formula for calculating surface area for their polyhedra and then provide a numerical answer for their SA Students individually will then answer the following probability questions about their dice. How many sides are there for each of the five regular polyhedra? What can you say about the names of the polyhedra? What is the probability of rolling a 1 for each die? If both dice are rolled at the same time, what is the probability that the sum of the dice will be 10? * Extension:  What is the probability that when both dice are rolled, two 5's will land. * Students will then bring in their creations and surface area answers, and display them in class for all students to see.
Sources (bibliography, websites, etc.)
Length of time project will take (in and out of class)	3 classes for assigning of pairs, polyhedra, and creation of polyhedra dice, and surface area formulas . Students should have enough classtime to finish their models and proceed to inquiry on probability, otherwise it is to be on their own time. 20 mins at beginning of one class to present and display
What students are required to produce	In pairs, two 3-D polyhedra dice models. Surface area formula and numerical answer Individually, answers to probability questions
Marking Criteria:

Part A.(In pairs)  Two 3D polyhedra paper model dice.  /20
                          Proper, correct construction of model
                          Creativity of design (colour, patterns etc)

Part B.(In pairs)  Surface area formula and calculation /15
                         Clear understanding of what surface area is and correct answers

Part C (Individual).  Probability inquiry and answers /10
                             
                             

Poetic Mathematics

Is it where we begin

Is it where we end

Or maybe it's where we collide

Thought of as nothing and emptiness

Yet its existence is crucial and necessary

Once considered to be a devilish sin

Now considered to be at par

Alive as a numerator

Dead as a denominator

Falling in the dimension of purgatory

Waiting to embark on a journey to either side of good and evil

Positive and negative

0 or Zero

Teacher Bird Comments:

I think this is a great tool/way we can incorporate poetry and writing into mathematics.  Both the free writing and Poetry spark creativity that mathematics can often lack.  Also, it is a good way of challenging those who aren't comfortable with writing.  On the other hand, for the math phobes it can be more comfortable and provide an alternative outlet.  Having multi-modal and interdisciplinary approaches is good way to display the "funner" side of mathematics!

Free write

zero, "nothing," location on a number line between -1 and 1, origin

 Divide, separating a group of people, numbers being divided by something, when there is a crack in something, division of sports teams like west versus east or north conference south conference west conference and then I don't know what to write about divide, two divided by one is two and eight divided by two is 4, it is the opposite of multiplication sort of, separating, parting, when you divide a group you are separating it into smaller groups.

zero, nothing, the origin, wasn't used/known in certain historical times, having no value, rating scale of 0 - 10 with 10 being the best and 0 being the worst.  We often associate zero with being a bad thing but in sports like golf it is a good thing :) lots of things have countdowns to zero, time in sports, liftoff, race's 3,2,1,GO! zero is a number inbetween -1 and 1.

Sponsor Teacher Response To Challenging Topics

In pre-calc 12, I think that permutations, combinations, and binomial theorem will be the most challenging and difficult for students to understand.  After emailing my sponsor teacher, she agrees completely.  Last year was her first year teaching this topic and she found that she had to go at a much slower pace than anticipated.  In addition, she had to explain the concepts with more detail and precision in comparison to other topics.  So some basic tips from her were to adjust the pace accordingly and to make sure students understand what information is key when reading word problems.

I think probability(perms, combs, binomial theorm) is a difficult topic in general because types of problems and the concepts are extremely different from what students are used to.  There are formulaic, logical, and common sense aspects to probability which make it difficult.  I think understanding what information to look for in word problems is a skill that needs to be developed so before introducing probability we should make sure to incorporate word problems throughout the year.  Also, the Khan academy had a couple of great videos on permutations and combinations that explain the concepts in a clear way.    

Lesson Plan for Microteaching in Partners - S.A. of Cylinders

Bridge: Each student is given a template of the cylinder and is asked to cut it out and build it.

Learning Objective: Students will learn to determine the surface area of a cylinder.

Teaching Objective: Students will build their own cylinders and in doing so, discover what contributes to the total surface area of a cylinder. Students will also learn the formula of a cylinder.

Pre-Test: Ask participants to work in groups of 4 and to find the surface area of the cylinder they have just cut out.

Activity:

Time	Teacher	Participants
2 min	Introduce topic and explain some of the practical applications of the S.A. of a cylinder.	Think about different applications of the surface area of a cylinder.
2 min	Ask participants to figure out the surface area of the cut out cylinder (pre-test)	Work out surface area of a cylinder
3 min	Explain the surface area of a cylinder and work out the formula with the class. Random fact: surface area and volume of a cylinder have been known since deep antiquity.	Listening to teacher.
5 min	Ask participants to work in groups of 4 on the cylinder worksheet.	In groups of 4, students will work on the worksheet.
3 min	Review and go over solutions for the cylinder worksheet.	Ask questions and check answers.

Post-Test: Participants will be able to check their understanding and knowledge when working on the worksheet and then checking it with the solutions provided at the end.

Summary: We will go through the formula of a cylinder again and ask if there are any questions from the group. 

Response to Boaler and Staples article

Although a bit lengthy, I enjoyed reading Boaler and Staples article as it gave some valuable data on the differences between the "standard" and "Railside" teaching styles.  The two main points of emphasis were on improving overall learning of mathematics, and creating/attaining an equitable environment.  I personally enjoyed reading about how Railside tried to reduce inequalities.  This is something that I previously thought was extremely hard to incorporate into a mathematics classroom but the teachers at Railside used some creative and effective pedagogy to attain this.  It basically boiled down to group work, collaborative discussion, multidimensional solutions, and justification for these solutions.  One idea that struck me was having groups work on a particular problem, then randomly picking one of the group members solution, if the solution was wrong then the rest of the group had to help out that individual.  This gave a sense of responsibility for the entire group.  In addition, the idea that

"high attaining students developed deeper understanding from the

act of explaining work to others,"

grabbed my attention because one of the math workshops I attended had a teacher from Oak Bay who was experiment with peer teaching and was having great success with it, despite it being somewhat controversial. I am quite intrigued by the idea of students teaching students because it potentially has great benefits for both students.  Overall the article presented some creative teaching tactics and they had solid evidence to back it up.

The actual study was done quite well in my opinion.  They had accurate numerical data, and even written feedback from students to back up their results.  They had a good sample size, duration, and methods.  In terms of weaknesses I couldn't see any major flaws in the study.  A minor weakness was the fact that Railside mathematics classes were half a year long where as the traditional schools were a year long.  I think the study could have been more accurate if they had another school that had half year math classes. Nonetheless I don't think the impact was that big as it just allowed Railside students the option of being able to take more math classes and get further ahead.  Also, the CAT 6 scores were significantly lower than the traditional schools but they justified this due to the language being unfamiliar to Railside students. A fairly legitimate argument in my opinion.

As a whole, I found their conclusions to be quite accurate and I found it difficult to come up with any arguments against them.

Chinese Puzzle Problem

"how many guests are there?" said the official.
"I don't know," said the cook, "but every two shared a dish of rice, every 3 shared a bowl of broth,
and every 4 a dish of meat."

There were 65 dishes in all
How many guests?

Lets start off letting x = number of guests.

We know that there are three different dishes - rice, broth, and meat.  And we know that the total amount of rice dishes, broth bowls, and meat dishes is equal to 65.

Looking at the first statement, "every two shared a dish of rice," we can deduce that every guest has half a dish of rice.  So x/2 = number of rice dishes.

From the next two statements we can deduce that
x/3 = number of broth bowls and
x/4 = number of meat dishes.

So now we can get an equation using the fact that there are 65 dishes in total.
number of rice dishes + number of broth bowls + number of meat dishes = 65
or
x/2 + x/3 + x/4 = 65

From there we can solve for x, which is the number of guests.

6x/12 + 4x/12 + 3x/12 = 65 (Finding a lowest common denominator)
13x/12 = 65 (adding like terms)
x = (65 * 12)/13
x = 60

We can also solve this problem by guessing and checking

Lets guess that there are 120 guests.  That means that there are 60 dishes of rice, 40 bowls of broth, 30 dishes of meat.

60 + 40 + 30 = 130 which does not equal 65.

But we can notice that 130 is double 65.  so our guess was off by a multiplication of 2.
therefore we know that there are 60 guests.

I chose 120 because the numbers work out nicely, but this should work for other numbers with some rounding.



Extensions:  Does it make a difference that this is a Chinese puzzle?  Is culture important in math?

I don't think in this specific problem it makes a difference that is a Chinese puzzle.  The terminology used was irrelevant in my opinion.  It could have been french fries, burgers, and milkshakes.  

But I do believe that culture is important in math.  I remember in highschool we were doing a section on probability and the teacher did an example of a football game.  It wasn't much of a problem to our class as everyone knew what football was and how it was played, but if there was some European students in the class they might not have fully understood the problem.

Introducing Algebra Into the classroom video

My initial reaction when the video started was..... seriously?

But soon after I realized what the teacher was trying to accomplish and he accomplished it quite effectively.  One of the parts that stuck out to me was when he introduced the negative numbers.  Tapping on the board from right to left, he went from 3,2,1,0,-1,-2,-3.  The students seemed to comprehend that.  However, shortly after that he started at -6 and then tapped the stick to the right.  Some students mumbled out -7, and some students mumbled out -5.  It is easy to see why students would get confused because it's hard for them to comprehend that -7 isn't actually greater than -6.  That moment, I think, really cemented what a number line was and how it worked.

It was interesting to me because he introduced so many mathematical concepts(number line, negative numbers, preliminary algebra) with only using the ability to count, and barely speaking at all.  Pretty much any student of any level could comprehend what was being taught.

Hewitt : Arbitrary and Necessary

I quite enjoyed Hewitt's article as it brought up some new perspectives on why and how we teach mathematics.  In particular, the idea of received wisdom caught my attention and it was explained clearly in the following example,

"If a teacher stated that the angles inside a triangle add up to half a turn rather than offering a task for students to become aware of this, then students are left with having to accept what the teacher says as true.  In this case, it becomes just another 'fact' to be memorised.  I call this received wisdom."  

This particular example stood out to me because I would have to believe that most mathematics is taught this way, or at least it was during my highschool career.  Providing this 'received wisdom' or arbitrary content simply just provokes a battle of who can memorize the best.  As Hewitt explains, there are arbitrary facts that we simply cannot avoid the need for pure memorization, such as the x before y explanation, or names of certain shapes, however when necessary facts are explained in an arbitrary way, it becomes a problem because then we aren't teaching mathematics at all.  While I tend to agree with what Hewitt was saying, I question that it's much easier said then done.  It is easy for me to see how a teacher can assist in memory, but it is hard for me see how a teacher can educate awareness.  It seems to me that in educating awareness, the teacher is barely doing any educating at all, rather they are just facilitating or directing?  The students are simply figuring things out for themselves?  This concept confused me a bit.  

I would like to see more examples of what Hewitt is doing to get a better understanding of the differences between teaching arbitrarily and teaching awareness.  The idea of received wisdom is definitely something I will keep in mind and I hope to find instances in my lessons where I can stray away from it when it is not needed.  

Teacher Change and development via research

After reading Robinson's article one of the ideas that struck me was videotaping yourself teaching as a means of self analysis.  Your perception of the teacher you want to be versus the teacher who you are is something that a video can display.  It is important to receive feedback from external sources, but it is equally, if not more important to receive feedback internally.  I also enjoyed the section on incorporating group activities into mathematics lessons as it seems to be a common emphasis throughout all of our education courses.  It is good to see some first hand experience and verification of this being extremely beneficial.

There are obvious problems that come with group work such as certain students contributing to much or to little, not being respective of other students opinions, of conversation begins to go off topic.  Robinson seems to tackle a lot of these problems by designating each student a responsibility within a group and getting students to complete a synthesis evaluation.  One question I would ask Robinson would be, are there other major problems you experience by incorporating group activities?  If so, how do you manage them?

How will I continue to develop as a teacher after the education program?  

One way I will continue to develop is by having an online presence.  I think the internet, social media, and technology are all great tools and resources for students and teachers.  It's a great way to bounce ideas off other teachers, find, use and tweak creative lesson plans, as well as it allows for an easier learning experience as you don't have to go through all the same hardships that other teachers already went through.  I have yet to attend any major conferences but I think going to these events, not only just the math specific conferences but other disciplines as well will be informative and help me keep up with the current pedagogical trends.

Also, I will try and get feedback from my students on a consistent basis.  Students are the reason why we teach so their input is the most important.  Being willing to change and manipulate lessons based on who I am teaching is something I will always try to do.

Mathematics education for democratic citezenship

After reading the Simmt article I agree with the fact that everything in today's society is quantified and numerical so it's important that our mathematics education prepares students for this and that it is also crucial to acknowledge and incorporate the fact that mathematics can be a tool to provide the necessary civic skills required in our society.  I think the main challenge and problem with mathematics is the fact that we are over concerned with correctness.  It's very authoritative in a sense.  The way we test, mark, and teach mathematics is for the most part all based on getting the right answer.  This creates an individually competitive scene which isn't necessarily a bad thing as competitiveness is a form of motivation(I think math needs students who are more motivated).  But it becomes a problem when we start isolating ourselves.  As teachers, and students, we should be promoting collaboration, communication, and conversation amongst each other, much like Simmt points out as one of her arguments for citizen education in mathematics. As Jacob Brownowski says, 

"It is important that students bring a certain ragamuffin barefoot irreverence to their studies; they are not here to worship what is known, but to question it." 

Students should be willing to challenge and confront ideas rather then just adhering to what the teacher said because he/she is in authority.  Seth Godin says in a similar fashion,  

"You have been brainwashed by school and by the system into believing that your job is to do your job and follow instructions."  

It's important that students learn both skills in my opinion.  Being able to effectively listen and execute what someone else is saying is a life skill that is important in the work force.  But at the same time students should be able to formulate their own opinions and reasoning.  One of the main ways I will teach for democracy is by trying to provide a less isolated environment by getting students to work together, sharing their knowledge with other students via discussion groups, mini presentations, or group research projects.  However, from personal experience, I know that group work can often be problematic as it is hard to delegate who does what and it often turns out to be a one man job.  I also think that technology can be used to teach for democracy.  Via technology we can post notes, videos, links to other resources etc.  This can allow students to learn at their own pace rather then having to struggle to keep up in class.  Also, through the use of blogs or other social networking it is easier for certain individuals to speak their thoughts and is simply better for overall communication.  I know from personal experience in highschool, raising your hand to say something was often very daunting.  Now we can sit behind our computer screens and think about what we really want to say and then ask.  I think technology provides so many opportunities but the problem is that not every student has the latest gadget or device.          

In Mathematics there are plenty of different methods to solve the same problem so we should be encouraging this, not limiting it.  It's important to get collaborative input from all students perspectives. Mathematics shouldn't be based on who is the best "memorizer" but I feel like this is exactly what is happening in Secondary Math.  It's a big contest to see who can follow and memorize the steps correctly.       

"My contention is that creativity now is as important in education as literacy, and we should treat it with the same status.” - Sir Ken Robinson

It is important that we acknowledge creativity rather then linear memorization.  However, the problem is that instrumental teaching is often easier and less time consuming.  But we shouldn't be content with the easy way out. 

Ill end this post with an interesting quote I found from another article speaking on democratic education

 "in the end, we universally teach mathematics in schools in order to educate students; we do not universally educate students in order to teach them mathematics" (For the Learning of Mathematics , Vol. 17, No. 3 (Nov., 1997), pp. 11-16).  

Family Relations Problem

Brothers and sisters Have I none, but that man's father is my fathers son
Assuming the speaker is male, what is his relationship to "that man"

This problem shouts at me to make a diagram.

First lets see who is in this problem.  We have the speaker(me or I), the speakers father, that man, and that man's father.

So lets draw those out

The problem asks for the relationship between the speaker(me) and That man.
Now lets take a look at the second statement, but that man's father is my fathers son

so that man's father = my fathers son = ME

The first statement also says the speaker has no brothers and sisters so we can conclude that "That man" is my son.

If students are struggling:
         -give them a better understanding of how family tree's work
         -drawing diagrams helps a lot

Extensions: Can you create a paradoxical or difficult statement using double,triple, quadruple negatives
one you could use with your students?

1.I found a funny clip of the big bang theory using quadruple negatives!

http://www.youtube.com/watch?v=NAjFgVM0y5o

2."I don't owe nobody on my team nothing"

3. 

A very special island is inhabited only by knights and knaves. Knights always tell the truth, and knaves always lie.

You meet two inhabitants: Zed and Alice. Zed tells you, `I am a knight or Alice is a knave.' Alice tells you, `Of Zed and I, exactly one is a knight.'

Can you determine who is a knight and who is a knave?

Microteaching reflection

My initial thoughts and reactions after microteaching were mainly positive.  Myself and my peers agreed that for the most part I covered all aspects of the lesson plan, though sometimes not thoroughly.  Personally I had troubles with creating a hook and having a good way of summarizing/concluding.  These are important as they are the first and last impressions of your lesson so it is something I will continue to get better at.

Some of the feedback I received on the strengths of the lesson included
"Payed attention and offered feedback to every individual student"
"Simple and focused and did not try to overload on information"

These are two things that I completely agree with.  Having a decent amount of coaching experience I know the importance of giving feedback on an individual level and offering different types of feedback(verbal and visual).  Also, keeping it simple and not overloading students/athletes with too much information is critical in my opinion.  You need time to develop each individual part of the puzzle before putting it together.

Some of the feedback I received on areas of improvement were
"more eye contact"
"demonstrated a bump with a ball"
"more obvious hook and summary"

I always thought I did a good job of making eye contact with everyone but clearly I was wrong!  I will definitely make more of an effort to make eye contact with each individual consistently.

I was supposed to demo the bumping technique with a ball but I completely forgot too! I did it without a ball but forgot to do it with a ball.  Maybe for next time I should take a quick glance at my lesson plan here and there just as a reminder.

And yes I completely agree with a more obvious hook and summary, I had already noted it as one of my weaknesses and I will continue to develop this aspect of my lesson planning.

One thing I noted was the inclusion of extra activities.  To my surprise, the athletes were quite good at executing the proper technique and had successfully done this faster then expected.  I had a couple other progressions to add in to the drill, which I did, but again they were quite good at adapting to the variations to my surprise.  So maybe for next time I should make sure to have a fair amount of variations and other drills I can do if they group is excelling.

Great learning experience overall and the assessments were a valuable tool.

Micro Teaching Volleyball Lesson Plan

Bridge: "Have you ever wanted to join in on that game of volleyball at the beach but are to shy because your skills aren't up to par?

Objectives:  Students/athletes will be able to effectively "pass" or "bump" a volleyball using proper technique

Teaching Objectives: To provide an experience that is outside their comfort zone

Pre Test: Verbal check to see what athletes already know about volleyball in general, and more specifically
what they know passing technique.  (1 min)

Participatory Activity:  (6 min)
                              - First demo the correct form and why we use this technique
                                        - knees bent and shoulder width apart, thumbs down, minimal arm and leg motion
                                        - we use this technique because it provides the greatest surface area for the ball
                                        - and because the ball already has enough energy to pop off
                              -Shadow repetitions (no volleyballs)
                              -Real repetitions (with volleyballs)
                                        - athletes make a single file line and are tossed a ball with expectations of executing proper technique and the ball being passed back to the tosser.
                                        - progressions are, tossed ball, flat driven ball, hard driven ball  

Post test - verbal review of key points to proper passing technique(1-2 min)

Summary - wrap up of what was taught today, answer any further questions (1 min)

Variations - if athletes are advanced, get them to pass back and forth between each other or challenge them even more by tossing the ball in various locations (far left, far right, behind, in front)

                                                          

Battleground Schools

I have had the opportunity to chat with a teacher sponsor for the volleyball team I coach at Richmond High Secondary.  She just started teaching grade 8 math this year and she said its absurd as to how uniformed her students are in math.  This idea of math phobia is problematic especially to elementary school teachers as they are more generalized.  The teacher sponsor said that often times elementary school teachers will just simply ignore and spend very few hours on mathematics because they themselves have "math phobia".  In her case there is a huge discrepancy between the background knowledge of students when the enter highschool.  It's hard to catch the "lacking" students up with the students who had a solid elementary teacher.  I am sure I will come across similar situations in my teaching career and I am unsure of where and how to begin attacking a problem like this?

After reading battleground schools article it is pretty clear that there has been an ongoing debate between progressive and conservative views of mathematics.  These concepts relate heavily to the relational and instrumental concepts we have inquired about previously in class.  Starting from the progressivist reform era we had an instrumental prevalence.  Dewey then came along and introduce a relational view and since then it has been a back and forth war between the two.  The main part that concerns me is the binary view.  There is no middle ground or grey areas.  Its all black and white(progressive and conservative).  Personally, I think the solution is a combination of both.  As a student, you need the practice, repetitions, strict methods etc.  But you also need the inquiry, abstract, and problem solving skills.  They compliment each other. 

This worries me from a teaching perspective. Does our curriculum allow incorporation of both progressive and conservative?  Do our textbooks do so?  Will I always have to go along with the norm at the present time be it progressive/conservative or am I constrained to just the one path? Also these cycles from left to right don't benefit teachers in anyway.  It becomes a problem if a teacher grows up being taught instrumentally but is then asked to teach relationally or vice versa.

I hope there will be enough time and breathing room to engage students from both sides of the coin but I feel as if I will be forced one way or the other.           

Weight Scale Problem

A market vendor sells herbs in whole number amounts from 1 to 40 grams.
Using an old fashioned 2 panbalance and just 4 weights, she can measure any amount needed.
what are the 4 weights?

This problem turned out to be quite the challenge for me.  Although not directly stated in the question it should be noted that weights can be put on either side at any given time.  So for example if you had a 10kg weight and a 15 kg weight you could put the 10 on one side and the 15 on the other, then add 5g of herbs to balance it.  So we know that we need to find 4 weights in which their additive, subtractive, and counter parts contain all integers from 1-40.

I assumed we needed a 1g weight.  I then made a chart with all the numbers on it from 1 - 40 just so I could keep in check which numbers I needed to get.

From there I did a very methodical but time consuming procedure to find out the answer.

Since we already have a 1g weight, we can cross off 1 from our list.  Now we need to satisfy 2.  We can do this by either adding another 1g weight(1+1 = 2), 2g weight, or 3g weight(3-1 =2).  I decided to go with 3 because it was the furthest away from 1.

So now we can cross off 1,2(3-1),3, and 4(3+1) from our list.

Next we want to cross off 5 from our list.  We can do this by adding a 2g weight(2+3=5), a 4g weight (4+1=5), a 5g weight, a 6g weight(6-1=5), a 8g weight(8-3=5), or a 9g weight (9-(3+1)=5).  I decided to go with 9 because it was the furthest away from 3.

So now we can cross off all the way from 1-13 because we have 1,3,9g weights.

5(9-1-3)
6(9-3)
7(9+1-3)
8(9-1)
9
10(9+1)
11(9+3-1)
12(9+3)
13(9+3+1)

Now we need to cross off 14-40.
We know that we need 4 weights that will add up to 40.  So if we already have 1,3,9 what do we need to get 40?  1+3+9+x=40
                          x=27

Now we can cross off all the numbers from 1-40 because we have 1,3,9,27g weights.

This was the only way I could think of approaching this problem and it happened to work out after a decent amount of time spent plugging and chugging.

After seeing the answer 1,3,9,27 it's clear that these are 3^0, 3^1, 3^2, 3^3.  I tried to find a relation/reason for that but I couldn't figure it out.

Teacherly notes

It might not seem obvious at first but being able to recognize that both sides of the pan can be used is clearly essential to this problem so I think this should be stated in the problem.  This problem was really difficult for myself so I don't know if I can really give too much teacherly advice.

An extension could be
A market vendor sells herbs in whole number amounts from 1 to x grams.
Using an old fashioned 2 panbalance
what are the minimum amount of weights needed to find to measure any amount needed?

Relational Understanding and Instrumental Understanding

After reading Skemps article I can see that both relational mathematics and instrumental mathematics have their pro's and con's.  In a perfect world I think most teachers would agree that relational mathematics is more beneficial to students in the long run.  It allows for better adaptation skills to new problems, offers alternate way's to solve problems, and is cemented in our memory for longer.  Those are just a few to name.   However, the problem is that the world is not perfect.  I don't think relational mathematics is practical from a teaching perspective.  There isn't enough time to describe the why's of every formula, our curriculum is to heavy to do so, and it's substantially harder to test for.  Also if we start to give up some in class time to teach relationally, then we must me giving up some time to teach other subject areas.  From a practical point of view, I think instrumental teaching is far more realistic.  In addition, Skemps states that instrumental mathematics is a quicker and easier way of boosting self confidence in students than relational!  I think self confidence plays a huge role in learning for any discipline, not just math.  This definitely appeals to me as a teacher candidate.  I hope to be wrong though, maybe we do have the time and resources to integrate relational understanding and I am just unaware of it?  And I am sure there are other methods of boosting self confidence in students than instrumental understanding.

Another point brought up in Skemps article was the fact that most teachers use instrumental mathematics and in obvious relation, most students have an instrumental understanding.  So how can we expect our teachers to be more relational if they themselves haven't been taught in a relational way?  Also should we even be thinking in such a binary way(Relational vs instrumental).  Maybe it's optimal to have a blend of both.  I am sure many teachers already teach in a blended fashion.  There are topics that are easily explained relationally and for those that are substantially harder they most likely resort to instrumental to meet curriculum standards in a timely manner.  So while I think that relational understanding is the most desired, instrumental understanding seems more practical and is suffice enough for most students.  Personally I hope to blend both into my teaching.

One final thought I had was that regardless of the way they students were taught, a lot of them may resort to a instrumental understanding anyways just because it is so much easier and quicker to learn that way.  So even if we try to teach relationally, students might learn instrumentally anyways.

True instrumental understanding :)

Memory & Autobiography

Throughout my years as a student I had 2 teachers who were the most memorable.

The first one was my grade 9 math teacher.  Every single class he would bring his guitar and play a tune for us for the first 3 or 4 minutes of class.  To this day I still don't know the "educational" purpose of it.  Maybe it was to calm us down, get our attention, maybe it was even some form of pavlovian conditioning, or maybe it was just the fact that he enjoyed playing the guitar.  Either way it was memorable.  One other thing that he did, whether on purpose or not, was he constantly made errors and mistakes.  He would write up a problem on the board, start doing it, and then halfway through he would realize that he was doing it wrong and he would start over.  It provided some much needed laughter and comfort in knowing that not everyone is perfect.

The second one was my grade 12 math teacher.  The way she taught was very structured, organized, simple, and for the most part pretty standard.  Nothing to fancy, nothing to dull.  But the main thing I remember is that she presented the concepts in such a clear way that I rarely found myself looking in the textbook or going on the internet for a better understanding.  Maybe the concepts were just easier in grade 12?  Or maybe I just started trying harder? But I find it weird that I struggled so much in grade 8 but had no problems in grade 12.  If there is anything I have gained from her, it's that sometimes less is more.  I think as teachers we often get caught up and want to do too much.  From a students point of view this can be overwhelming and stressful so we need to take a step back and keep it simply.  Although my grade 12 teacher may have been pretty "standard," the clarity she provided was unlike any other.   

1000 Lockers and 1000 Students!

A school has 1000 lockers and 1000 students on the first morning of term, all the lockers are open.
Everystudent walks in one by one.
The first student walks in and closes every locker
student number 2 opens every second locker
the third student changes the state of every third locker(opens the closed ones and closes the open ones)
4th student changes every 4th locker... and so on

Once all 1000 students have completed this process, which lockers are closed and why?

First of all lets take a look at what it takes for a locker to be closed or open.  

For a locker to be open we need it to be changed an even number of times because all the lockers started open.  For a locker to be closed we need it to be changed an odd number of times.

So if we changed a locker an even amount of times, lets say 4 times, then it would 

open(because every locker starts open)

closed(1st time changed)

open(2nd time changed)

closed(3rd time changed)

open(4th time changed)

If we changed a locker say 3 times it should be clear that it would end up closed.

So now we need to figure out which lockers will be changed an even amount of times vs the lockers that will be changed a odd amount of times.

Lets take a look at a couple of examples to try and tackle this

Take locker 10 for example.

We know that locker 10 started open (because every locker started open), then it was closed because student #1 closed it, then it was open because student #2, then closed because of student #5, and then finally opened because of student #10.  Each locker is changed by the number of factors(he numbers it is divisible by) it has.  So 10 has factors (1,2,5,10).  Because this is an even amount of factors, in our case there is 4, we know that the locker will end up open.

Now take locker 16 for example.  We know its factors are (1,2,4,8,16).  This is an odd number so we know the locker will end up closed.

How do we know which numbers have an even amount of factors? And which ones have an odd amount?

To answer that we need to look at how factors work.  

Every number has factors that are paired up.  So for example 10 has (10x1,1x10,2x5,5x2).  These pairings produce an even number of factors.  Can you think of a case in which this isn't always true?  If you are having trouble, take a look at the number 16 for example.  16 is a perfect square so we have all the pairs plus the square itself. So 16 has (1x16,16x1,8x2,2x8) and (4x4).  In all the other cases the factors are paired up, producing an even number.  With perfect squares we get an odd number because the factors are paired up except for the square itself.  Still don't get it?  The image below may help you understand it a bit better!

So in conclusion all the numbers that are perfect squares will be closed so 1,4,9,16,25......961.  

and every non perfect square will be open.

Some teacherly notes:

If students are having trouble I think it would be a good idea to pair them up or set them into groups.  This task seems better suited for teamwork!

To challenge your students you can ask them other relevant questions such as
How many times does locker x get changed / touched?
Which locker gets changed the most?
Which locker/s are touched exactly 4 times? etc.

TPI response

To start things off, the results of my TPI test were as follows.

Nurturing was scored the highest(Dominant Perspective)
Apprenticeship and transmission were second highest.
Developmental and Social Reform were the lowest. (Recessive perspective)

I think Mathematics is a very intimidating subject. One of my goals as a teacher is to rid students of this intimidation factor and to inform them that making mistakes and going through failure happens to everyone  so providing a nurturing environment is key.  Lots of students lose self-confidence and self-esteem because of failure and making mistakes, but all of the most well known mathematicians have gone through several failures before achieving success.  Often times without failure there would be no success.  I think that is why I scored so high on the nurturing perspective.

I was surprised my developmental score was so low simply because I hope to be a teacher that gets to know my students on a personal level.  I want to be able to adapt to my students ways of thinking and their level of knowledge.  This is very important to me.  So I am not sure why I scored low?  Maybe I am just not as familiar as to how I should achieve this in a classroom setting?
I think I scored lowest on social reform because I put more emphasis on providing qualitative content in an effective and clear way rather then putting am emphasis on social values and ideologies.  I think Other disciplines such as social studies or English have an easier time of putting more value into social reform.  But again, I hope to learns ways in which I can use this in my lessons as I am unclear as how to do so currently.  The best thing about being a teacher, or becoming a teacher is that we are always evolving as we learn more.

 

Response to Thurston's Article

After Reading Thurston's article I think the main thing I appreciated was his emphasis on communication. Not only in the way we present mathematical concepts but also in a social setting. As Thurston says “Human thinking and understanding do not work on a single track” Different methods of communication benefit different types of people in different ways. I will definitely try to utilize different methods of communicating into my classroom by adding visuals, using metaphors, analogies, and incorporating “motion.” Another point made by Thurston that stood out to me is that its important we don’t assume prior knowledge as this may cause unwanted barriers. Not everyone has the same “mathematical mental infrastructure.” We as teachers need to identify and react to this accordingly by putting a greater emphasis on educating the basics of math and using effective means of communication. Also we need to enjoy the social settings of mathematics! I think too often we get into a narrow minded way of thinking and we treat math as a solo project. We should be expressing our ideas to other people and digesting theirs. Using a social environment to our advantage.

One of the big points that caught my attention was how Thurston implied that most people didn't really care much about the actual proof itself, or rather the results. However it was the understanding that played a greater importance. I’m on the fence to agree if that is still true in an elementary or secondary setting? In my experience, a lot of students just simply want to know the answer :)

Nonetheless I have a different outlook on why we teach and how we should teach mathematics. Putting more of an importance on things that I otherwise would have neglected.

Newspapers and Math??

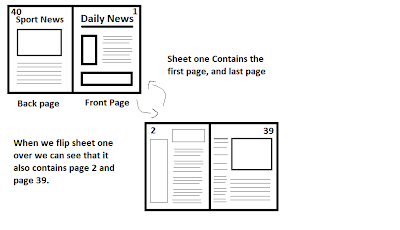
In reading a newspaper, you notice that 4 pages of a section are missing.  One missing page is pg.13.  The back of this section is pg.40

What are the other 3 missing pages?

My first step was to figure out what a newspaper is and how the pages are organized.  A newspaper is constructed by stacking sheets of paper on top of each other and then folding it in half.  Therefore each sheet  of paper contains 4 pages.  Having a hard time visualizing this? Simply grab a few pieces of paper, stack them on top of each other and then fold it in half.
So in our example this first sheet would contain pages 1,2,39, and 40.

Now that we know how a newspaper actually works lets tackle the problem at hand.

Since 40 pages is a relatively low number we can just work our way through all the sheets until we get to page 13

We already know the first sheet contains pages (1,2,39,40).  So the second sheet will contain (3,4,37,38)
and so on
(5,6,35,36)
(7,8,33,34)
(9,10,31,32)
(11,12,29,30)
(13,14,27,28)

So our answer would be pages 14,27,28!
Easy enough.
But what if we said there was 1000 pages and one missing page was page 217?  So the first sheet would contain pages (1,2,999,1000) and we need to find out (217, ?, ?, ?)

I'm way to lazy to write out each section one by one!

Here's a faster way.  We should be able to see that page 218 will also be included because the starting page of each sheet contains the next page as well. Also based on our previous example, page 5 goes in hand with page 6, page 7 with 8, all the way to page 217 with 218.  So now we have (217,218, ?, ?).  We can figure out the rest easily if we just subract 217 from the last page.  1000-217 = 783.  And then we can figure out the last page because 783 goes in hand with 784.

so we get (217,218,783,784)

We can do this subtraction because we already know how a newspaper is organized.  However many pages we go in from the front must mean we go the same amount of pages from the back.

A few words of teacherly advice:

If a student is having trouble
            - I think most students would have trouble visualizing how the newspaper is organized.  So if that is the case then simply just bring in a physical newspaper and show them!
           

Some ways to extend this problem
            - Increase the page numbers
            - Try removing a page that is past the "halfway" mark


           
       

           

Thoughts on proofs

Is Mathematical proof important in mathematics? Why/why not?

Is Mathematical proof important in secondary school math teaching & learning? Why/why not?

I think proofs play a very important role in mathematics.  Its how we can show our peers, colleagues and ourselves that a concept or theory is in fact true.  Proofs are the basic building blocks of math.  We need to be able to understand and use proofs so that we can build and expand on them.  Everything in math builds and relies on eachother, there is a lot of crossover between different fields of math. Proofs make us able to do just that.

Is it important in secondary education? I'm not so convinced that it is absolutely necessary but it's definitely something that we should try to incorporate into our lessons.  Secondary students are always curious as to why we do certain things in math?, why certain concepts are true?  And its important, if we can, to explain to them why.  Sometimes though proofs can be too complex for even a teacher to fully understand let alone a student.  While it is vital to mathematics, it is not vital to secondary education.  If and when we can use proofs in an understanding matter to students we should do so.  But being able to learn the fundamentals and concepts in secondary math doesn't rely on proofs.

First Assignment!

How many sqaures in a 8x8 chessboard?


My thought process behind this was to first identify which types of sqaures could possibly be in the chessboard.  Everything from a 1x1, 2x3, 3x3...... to an 8x8 sqaure. The next step was to figure out how many of each type there are. Once we do that we can simply add them up to get our answer!

For starters I looked at the 1x1 type squares.  It's pretty clear that there is a total of 64.  The reasoning is because there are 8 possible positions vertically and 8 possible positions horizontally.  8x8 = 64.


I applied this same method to all of the different types.  So for a 2x2 type we can see that there is 7 possible positions vertically and 7 possible positions horizontally.  We are limited to 7 because we would go "outside" the board otherwise.  so 7x7 = 49

After applying this method to all types, I ended up with

64 1x1's
49 2x2's
36 3x3's
25 4x4's
16 5x5's
9  6x6's
4  7x7's
1  8x8's

Add them all up and you get 204!

A few words of teacherly advice:
 For students who are stuck or having a difficult time:
               - Add a visual representation or visual aid, this helps a lot!
               - Show them that there is more then just 1x1 squares, 64 is not the answer!

Ways to expand this problem:
               - What happens if the 8x8 chessboard gets bigger or smaller? (ex. 7x7 or 9x9)
               - Other shapes(rectangles, triangles)

Hope you all enjoyed

Thanks :)

First blog

Hey everyone this is my first blog post